Si r est la longueur du rayon de (C), celle du rayon du cercle (C') commun à tous les triangles équilatéraux inscrits est
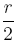 .
.La longueur de la corde [AB] est déterminée par la position de son milieu I. Choisir une telle corde revient donc à se donner un point au hasard à l'intérieur du cercle.
La probabilité que la longueur de la corde soit supérieure à celle du côté du triangle équilatéral inscrit est alors égale à la probabilité que le milieu de la corde soit intérieur au cercle (C') de rayon moitié, inscrit dans ce triangle.
En effet, la distance du milieu I de la corde au centre O du cercle ne doit pas excéder le rayon du cercle (C').
Si r est la longueur du rayon de (C), celle du rayon du cercle (C') commun à tous les triangles équilatéraux inscrits est 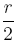 .
.
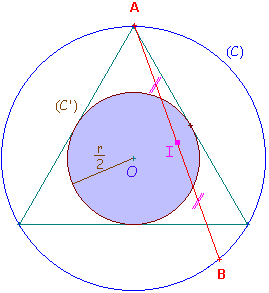
La répartition de ce point étant uniforme dans le cercle, la probabilité demandée est le rapport entre l'aire du cercle (C') et l'aire du cercle (C).
D'où la probabilité demandée :
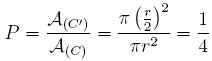 .
.
Afin de vérifier l'exactitude de la probabilité trouvée lors de la modélisation de cette troisième approche, le site TrigoFACILE a mis au point un algorithme qui permet de simuler la position du milieu d'une corde tracée au hasard dans un cercle.
Testez cet algorithme sans plus tarder en indiquant dans la case ci-dessous le nombre d'itérations désirées puis cliquez sur le bouton de validation.
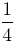 .
.
Théorie et expérience se rejoignent encore une fois !
C'est donc que cette troisième approche nous suggère une nouvelle réponse, différente des deux premières, au paradoxe de Bertrand, qui par la même occasion se complique à nouveau.
Et pourtant... Une nouvelle suprise nous attend !
Cliquez ici pour poursuivre l'étude de ce paradoxe...
↑ Retour au haut de cette page