Introduction

Une
partie seulement de cet exposé est présent sur le site. La version complète, qui comprend la
démonstration intégrale de la validité de l'algorithme AKS, n'est disponible que dans le fichier rédigé à l'aide d'AMS-LaTeX, téléchargeable dans
une version PDF 
pour en faciliter la consultation et l'impression.
Une version allégée de cet exposé est aussi parue dans le soixantième numéro du
magazine de mathématiques pures et épicées Quadrature (avril–juin 2006, édité par
EDP Sciences).
Intérêt de l'algorithme
Les nombres premiers jouent un rôle fondamental en mathématiques et possèdent moult applications très utiles de nos jours, notamment dans le domaine de la cryptographie. Il est donc intéressant d'établir des tests pratiques et fiables de primarité.
Depuis l'invention de la théorie de la complexité dans les années 1960, le problème que nous noterons P, qui est de savoir si un nombre donné n est premier, passionne les chercheurs.
Le tableau ci-dessous dresse la liste chronologique des algorithmes majeurs qui ont été trouvés afin de déterminer la primarité d'un nombre.

Bien que des progrès aient été réalisés au fil des années, seul le dernier algorithme vérifie en même temps les trois critères présentés et qui sont détaillés infra.
Tout entier n composé possède une preuve très courte de non-primarité, à savoir un diviseur non trivial. Alors qu'il est très difficile d'exhiber les facteurs premiers des grands nombres, il est assez aisé de vérifier qu'un certain nombre en est bien un facteur premier : on dit alors que P est un problème de classe co-NP où NP désigne la classe des problèmes qui peuvent être résolus en temps polynomial par un algorithme non déterministe – il suffit en effet de simplement effectuer la division avec le facteur magiquement exhibé –, le préfixe « co » signifiant que c'est le problème complémentaire de composition des nombres qui est considéré.
De plus, pour peu que l'on connaisse la décomposition en facteurs premiers de n-1, un critère de Lehmer énonce que si, pour un entier a, 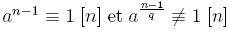 pour tout diviseur premier q de n-1, alors n est premier, ce qui montre que P est un problème de classe NP.
pour tout diviseur premier q de n-1, alors n est premier, ce qui montre que P est un problème de classe NP.
Or, les mathématiciens souhaiteraient aller plus loin et prouver que P est un problème de classe P, où P désigne la classe des problèmes décisionnels, c'est-à-dire auxquels l'on peut répondre par « oui » ou par « non », qui peuvent être résolus par un algorithme déterministe en temps polynomial quel que soit l'argument n du problème.
L'algorithme AKS est la preuve cherchée, ce qui établit le résultat fondamental :
P est un problème de classe P.
Et c'est ce problème de longue date qui vient d'être résolu en août 2002 par le professeur Manindra Agrawal et deux de ses élèves, Neeraj Kayal et Nitin Saxena, qui viennent d'obtenir leur licence dans le Département d'Informatique de l'Institut Indien de Technologie à Kanpur. Une seconde version améliorée de cet algorithme « brillant, élégant et simple » a ensuite été présentée en mars 2003. Cette nouvelle version est plus élégante et ne requiert pas de résultats pointus d'algèbre afin d'être démontrée dans son intégralité.
Par ailleurs, un intérêt non négligeable de l'algorithme AKS est qu'il ne nécessite que quelques outils assez simples d'algèbre afin d'être démontré, ce qui est loin d'être le cas pour les autres algorithmes de primarité qui font appel à des résultats très pointus en théorie des nombres.
L'importance du résultat présenté dans cet exposé est que l'algorithme AKS garantit l'obtention en un temps polynomial d'une réponse catégorique sur la primarité d'un nombre. De fait, cet algorithme se démarque de tous les autres puisqu'il réunit les trois critères fondamentaux que nous allons maintenant préciser plus en détail.
Un algorithme déterministe
L'algorithme AKS est déterministe, en ce sens qu'il détermine toujours pas un « oui » ou par un « non » définitif et sans erreur possible la primarité de l'entier donné. Mais il est plus facile de définir ce qu'est un algorithme déterministe par la négation de la nature d'un algorithme probabiliste.
Celui-ci peut faire partie de deux types :
- les tests de composition qui permettent de déterminer de manière sûre si un nombre est composé, sans pourtant nécessairement en fournir une décomposition explicite ;
- les tests de primarité, nettement moins rapides, qui permettent de déterminer de manière sûre si un nombre est premier.
Lorsque le test ne retourne pas une réponse catégorique, la probabilité de primarité ou de non-primarité du nombre est d'autant plus élevée que l'algorithme effectue d'itérations. Par exemple, pour le test de Solovay-Strassen, il est démontré qu'il existe un entier a premier avec n sur deux qui ne vérifie pas le test ; aussi, en réitérant k fois l'algorithme avec des entiers a différents choisis au hasard, la probabilité d'erreur sur la primarité de n est-elle de l'ordre de 2-k, s'il satisfait à chacun de ces tests, que l'on admettra indépendants. Ainsi, pour 50 itérations de ce test, le risque d'erreur est inférieur à 10-15.
En pratique, les tests probabilistes de primarité actuels ont une probabilité d'erreur inférieure, dit-on, à la probabilité que le système informatique qui réalise le test commette une erreur tandis que dans la même minute son utilisateur remporte la cagnotte à la loterie et meure foudroyé ! Nonobstant, l'erreur est toujours en théorie possible, si bien que les mathématiciens essaient depuis de nombreuses années de la supprimer.
En outre, les algorithmes probabilistes utilisent des séquences de tests aléatoires à chaque utilisation, de telle sorte que des réponses différentes peuvent survenir lors du test du même nombre, ou l'algorithme peut tout simplement ne pas aboutir. Au contraire, un algorithme déterministe produira toujours la même séquence d'opérations pour le même argument fourni.
Un algorithme en temps polynomial
L'algorithme AKS donne une réponse en temps polynomial, en ce sens qu'il existe un polynôme P tel que, pour tout entier n, l'algorithme exécute au plus P(log(n)) opérations élémentaires pour fournir le résultat, lorsque la donnée initiale est le nombre n. On convient que si n = 0, P est le polynôme nul.
La complexité temporelle de l'algorithme est donc une fonction polynomiale en le nombre de chiffres nécessaires à représenter n, que ce soit log10(n) en base décimale ou log2(n) en base binaire.
À l'ère des micro-ordinateurs, de tels algorithmes sont considérés comme implémentables, à la différence des algorithmes en temps exponentiel inutilisables en pratique, puisque le temps de calcul devient rapidement trop important lorsque le nombre à tester devient grand.
Bien qu'il soit facile de prouver la complexité temporelle de l'algorithme AKS en Ω(log(n)10.5), il est aussi possible de trouver une meilleure complexité en Ω(log(n)7.5) grâce à des résultats de théorie des nombres.
Toutefois, cela reste encore assez lent étant donné que l'on estime que les algorithmes réellement utilisables doivent être au plus en Ω(log(n)3).
Cela n'a cependant aucune incidence sur le résultat théorique que P est un problème de classe P.
Un algorithme inconditionnel
L'algorithme AKS ne repose sur aucune hypothèse : sa validité, tout comme sa complexité temporelle polynomiale, sont entièrement prouvées et ne font pas appel à des conjectures de théorie des nombres, à la différence de la majorité des autres tests de primarité. Notons toutefois que si l'hypothèse de Riemann généralisée était démontrée, on aurait déjà prouvé avec l'algorithme de Miller-Rabin en temps O(log(n)2) que P est un problème de classe P, mais le fait est que cette conjecture n'a toujours pas été prouvée.
↑ Retour au haut de cette page
 Une partie seulement de cet exposé est présent sur le site. La version complète, qui comprend la démonstration intégrale de la validité de l'algorithme AKS, n'est disponible que dans le fichier rédigé à l'aide d'AMS-LaTeX, téléchargeable dans une version PDF
Une partie seulement de cet exposé est présent sur le site. La version complète, qui comprend la démonstration intégrale de la validité de l'algorithme AKS, n'est disponible que dans le fichier rédigé à l'aide d'AMS-LaTeX, téléchargeable dans une version PDF  pour en faciliter la consultation et l'impression.
pour en faciliter la consultation et l'impression.
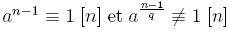 pour tout diviseur premier q de n-1, alors n est premier, ce qui montre que P est un problème de classe NP.
pour tout diviseur premier q de n-1, alors n est premier, ce qui montre que P est un problème de classe NP.