Par l'intermédiaire de cette activité préparatoire, nous allons définir comment un plan peut être orienté.
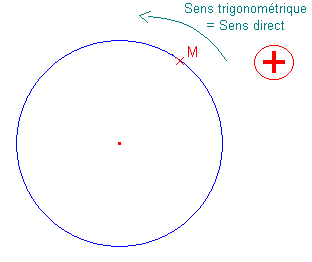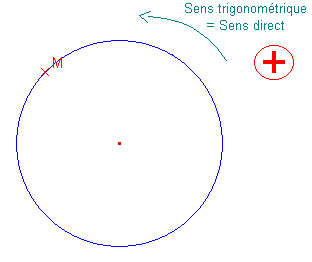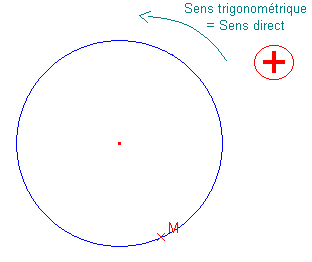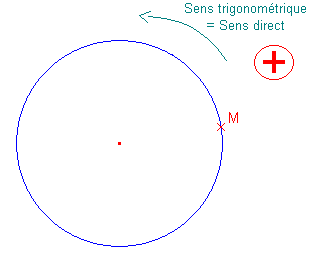
Pour cela, considérons un cercle et un point M placé sur le cercle.
Nous savons qu'un cercle est constitué d'une infinité de points. De plus, tout cercle est parfaitement défini par la donnée de son centre et de son rayon.
C'est donc que le point M peut engendrer le cercle tout entier en se déplaçant, tout en restant à la même distance du centre du cercle.
Les animations ci-dessous représentent ces deux possibilités.

Dans ce premier cas, le cercle est dit orienté dans le sens :
Toutes ces appellations désignent le sens inverse des aiguilles d'une montre – encore dit le sens « SIAM ».
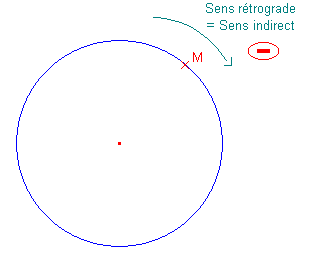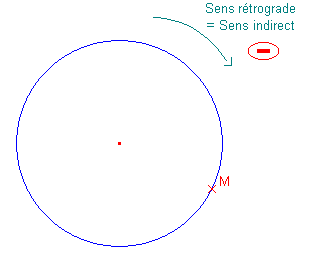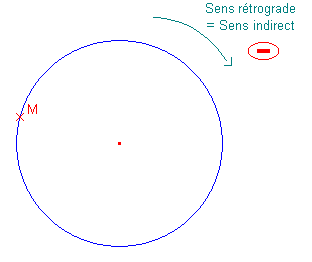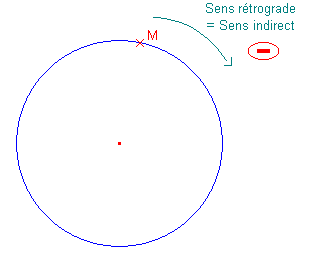
Dans ce second cas, le cercle est orienté dans le sens :
Toutes ces appellations désignent le sens des aiguilles d'une montre – encore dit le sens « pas SIAM ».
Orienter un cercle, c'est faire le choix d'un sens de parcours, appelé sens direct ou sens indirect.
Orienter le plan, c'est faire le choix du même sens de parcours pour tous les cercles du plan. D'ailleurs, dès qu'un cercle est orienté, tous les autres cercles du même plan sont orientés de la même manière.
↑ Retour au haut de cette page