Par l'intermédiaire de cette activité préparatoire, nous allons définir la fonction qui est appelée cosinus d'un angle aigu.
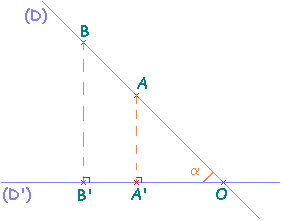
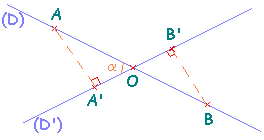
Pour cela, considérons deux droites (D) et (D') sécantes en un point O et l'angle aigu α formé par ces deux droites.
Plaçons en outre deux points A et B sur (D).
Puis notons A' et B' leur projeté respectif dans la projection orthogonale sur (D'), c'est-à-dire :
D'où (AA') // (BB').
La figure ci-dessous représente cette construction.
Posons OA = 2 cm et OB = 3 cm, d'où AB = 1 cm.
Mesurons alors la longueur des segments [OA'] et [OB'] pour différentes configurations.
Pour α = 60°, on a :
.
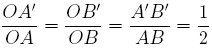Pour α = 45°, on a :
.
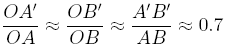Le rapport A'B' sur AB, noté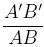 
, ne dépend pas des points A et B de (D). Ce rapport dépend de l'angle α formé par les deux droites (D) et (D').
Soient deux droites sécantes (D) et (D') formant un angle aigu α. Considérons A et B deux points quelconques de (D) et notons A' et B' leur projeté respectif dans la projection orthogonale sur (D').
Le rapport 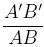est appelé cosinus de l'angle α.
Nous notons alors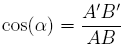 
.
Ce rapport est toujours valable dans la configuration ci-dessous.
En limitant l'application de la fonction cosinus au triangle AOA' rectangle en A', nous vérifions que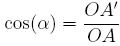 
.
Nous en déduisons ainsi la propriété fondamentale :
.
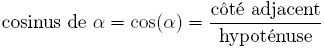Les égalités établies précédemment entre les rapports des longueurs pouvaient aussi être déduites du théorème de Thalès et des propriétés de la projection.
On utilise encore parfois la fonction trigonométrique sécante définie comme l'inverse du cosinus :
.
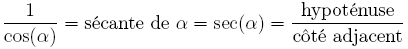↑ Retour au haut de cette page