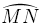 dont la longueur est le tiers de celle de la circonférence du cercle (C).
dont la longueur est le tiers de celle de la circonférence du cercle (C).Par raison de symétrie, nous pouvons supposer que l'une des extrémités de la corde a été fixée en un point A choisi aléatoirement sur le cercle (C).
L'autre extrémité B sera choisie au hasard sur la circonférence.
La probabilité que le point B tombe sur un arc donné de la circonférence étant proportionnelle à la longueur de cet arc, la corde est plus longue que le côté [MN] du triangle équilatéral inscrit dans le cercle lorsque B se trouve sur l'arc 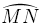 dont la longueur est le tiers de celle de la circonférence du cercle (C).
dont la longueur est le tiers de celle de la circonférence du cercle (C).
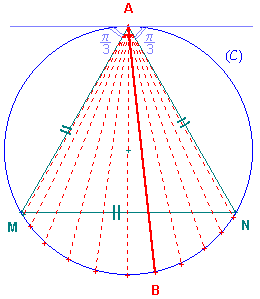
Puisque le triangle équilatéral, tout comme le sommet A, détermine trois arcs isométriques, la probabilité P cherchée est :
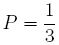 .
.
Afin de vérifier l'exactitude de la probabilité trouvée lors de la modélisation de cette deuxième approche, le site TrigoFACILE a mis au point un algorithme qui permet de simuler la longueur d'une corde tracée au hasard dans un cercle.
![[pi/3 ; 2pi/3]](/maths/curiosite/paradoxe/bertrand/images/ap2_intervalle.png) .
.
Testez cet algorithme sans plus tarder en indiquant dans la case ci-dessous le nombre d'itérations désirées puis cliquez sur le bouton de validation.
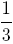 .
.
Théorie et expérience là aussi se rejoignent !
C'est donc que cette deuxième approche nous suggère une nouvelle réponse au problème de Bertrand, qui devient de fait un véritable paradoxe.
Et ce n'est pas fini...
Cliquez ici pour poursuivre l'étude de ce problème avec une troisième approche.
↑ Retour au haut de cette page