

Et si une droite tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces deux droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.
Ce cinquième et dernier postulat est le plus célèbre de tous les Éléments d'Euclide, si bien qu'il est souvent appelé « le postulat d'Euclide ». Cependant, son énoncé exact est la plupart du temps inconnu par ceux qui citent ce postulat, aussi dit « postulat des parallèles ». Nous verrons infra que le postulat « par un point extérieur à une droite donnée, ne passe qu'une unique droite qui lui est parallèle » – qu'Euclide n'a jamais écrit – n'est qu'une conséquence du vrai cinquième postulat énoncé ci-dessus.
Cet énoncé a priori obscur cache en fait une réalité toute simple ; cela devient même une évidence lorsque nous considérons un dessin. Ce postulat ne s'applique que dans un plan déterminé : les droites doivent être coplanaires. En fait, il suffit de considérer deux droites (D) et (D'). Une sécante (AB) à ses deux droites forme les angles « intérieurs du même côté » marqués en orange sur le dessin. La somme des mesures de ces deux angles est inférieure à la somme des mesures de deux angles droits, c'est-à-dire 180° ; en conséquence :
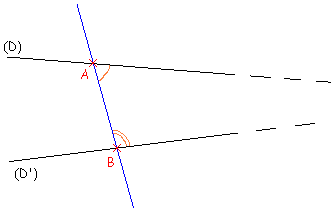
Il va de soi que lorsque la somme des deux angles est supérieure à celle de deux angles droits, les droites sont sécantes en un point situé dans le demi-plan délimité par (AB) et ne contenant pas les deux angles considérés.
C'est là où intervient le talent, ou le génie, d'Euclide : une trivialité « matérialisable » ne lui paraît pas suffisante pour être posée comme une notion première, dans une construction où c'est la logique qui doit convaincre. Tout en étant nécessaire à l'édification des propositions à venir, elle ne peut être posée comme allant de soi.
Le cas particulier provient lorsque la somme des deux angles est égale à celle de deux angles droits, ainsi que le montre la figure ci-dessous, dans laquelle les deux droites (D) et (D') ne sont alors plus sécantes : elles sont parallèles.
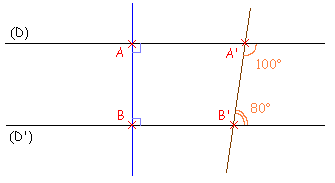
Revenons maintenant sur ce « postulat des parallèles ». Cette appellation provient du fait que ce cinquième postulat peut être utilisé pour prouver des propriétés inhérentes aux droites parallèles. Paradoxalement, le mot « parallèle » ne figure à aucun moment dans le postulat d'Euclide. Toutefois, cette appellation est due au fait que plusieurs énoncés équivalents et plus simples peuvent en être donnés, comme par exemple :
Ce sont autant d'hypothèses qui, sous forme affirmative, sont équivalentes.
C'est toutefois sur la dernière formulation que s'est déterminée la tradition pédagogique depuis deux siècles ; nous la devons à des auteurs anglais qui l'utilisèrent les premiers. Elle fut fixée avec succès à partir de la parution en 1795 d'une édition scolaire d'Euclide due à l'Anglais John Playfair (1748-1819). D'ailleurs, dans les pays anglo-saxons, le « postulat d'Euclide » se dit « postulat de Playfair » !
Historiquement, ce postulat est le plus intéressant de toute la géométrie, en ce sens que les géomètres de toutes les époques n'ont cessé de s'interroger sur la possibilité de démontrer ce cinquième postulat à partir des quatre autres postulats et des définitions, de manière à pouvoir établir la géométrie euclidienne sans qu'il soit nécessaire de poser ce postulat comme tel. Le procédé employé était souvent la démonstration par l'absurde : en considérant cette cinquième demande comme fausse, il s'agit d'arriver à une contradiction avec les autres postulats, les définitions ou les notions communes. Il advint que beaucoup de déductions étranges furent obtenues par le simple fait de nier ce postulat, si bien que nombreux furent les géomètres à penser que de telles absurdités impliquaient nécessairement que le postulat d'Euclide dérivât des autres, en ce sens qu'il n'était nul besoin de le poser comme tel : ce ne serait alors plus un postulat, mais une propriété qui découle des autres postulats.
Néanmoins, de telles absurdités ne sont pas obligatoirement des contradictions puisque rien ne disait l'opposé – selon le sens étymologique de « contradiction » – des autres faits établis. Et si des tentatives de démonstrations directes réussissaient, c'était parce qu'elles utilisaient implicitement, et sous une autre forme, ce postulat même qu'elles tentaient d'établir.
Le jésuite italien Giovanni Girolamo Saccheri (1667-1733) publia l'année de sa mort un traité intitulé Euclides ab omni naevo uindicatus, ou Euclide libéré de toute tache, dans lequel il aboutit à l'indépendance du cinquième postulat par rapport aux autres. Si, sur un segment [AB], l'on élève des perpendiculaires en A et en B, et si l'on prend sur chacune des segments [AD] et [BC] de même longueur, on démontre aisément à l'aide de propositions établies par Euclide et n'utilisant pas encore le cinquième postulat, que le quadrilatère obtenu a d'abord les propriétés d'un trapèze isocèle, c'est-à-dire que les angles en C et en D sont égaux.
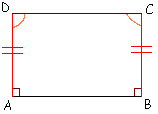
Il reste à examiner la nature des angles C et D de ce quadrilatère dit « quadrilatère de Saccheri » : si, en les considérant aigus, ou obtus, naît une contradiction, lesdits angles ne peuvent qu'être droits. Saccheri montra alors que les deux hypothèses sont incompatibles avec les postulats euclidiens puisqu'elles le conduisent à deux conclusions qu'il estima non admissibles : la première, à l'existence d'une perpendiculaire commune à deux droites à l'infini, et la seconde, à l'affirmation que deux droites contiennent un espace. Il finit ainsi par dire que ses conséquences « répugnent à la nature de la ligne droite ». Néanmoins, le mathématicien suisse Johann Heinrich Lambert (1728-1777) était en 1766 plus hésitant dans le cas de l'angle aigu, bien qu'il rejetât aussi l'hypothèse de l'angle obtus.
Or, il se trouve que, s'édifiant à partir de chacune des hypothèses précédentes, des géométries exemptes de contradictions sont possibles.
Ce n'est qu'au début du dix-neuvième siècle que des géométries non euclidiennes apparurent, en n'admettant pas le cinquième
postulat :
la géométrie hyperbolique sur des surfaces à courbure constante négative du Russe Nicolaï Ivanovitch Lobatchevski (1792-1856), du Hongrois János Bolyai (1802-1860) et de l'Allemand Carl Friedrich Gauß (1777-1855) utilise le fait qu'il y ait une infinité de parallèles passant par un point extérieur à une droite donnée.
La nouvelle version de ce postulat est d'ailleurs équivalente à « la somme des angles d'un triangle est inférieure à deux droits ».
Notons au passage que Gauß inventa cette géométrie sans « oser » la publier, craignant « les clameurs des Béotiens » et que Bolyai, qui la découvrit à l'âge de vingt ans, fut tellement déçu d'apprendre que les deux autres avaient déjà avancé leurs recherches sur ce sujet qu'il ne publia plus aucune œuvre mathématique !
Par ailleurs, il paraîtrait qu'au voisinage des trous noirs, l'espace n'est plus euclidien, mais semble régi par la géométrie de Lobatchevski.
Dans la géométrie sphérique sur des surfaces à courbure constante positive de l'Allemand Bernhard Riemann (1826-1866), il n'existe aucune droite parallèle à une droite donnée passant par un point extérieur à cette droite.
La nouvelle version de ce postulat est d'ailleurs équivalente à « la somme des angles d'un triangle est supérieure à deux droits ».
Il n'en faut pas moins noter que l'Italien Eugenio Beltrami (1835-1900) prouva qu'une géométrie non euclidienne ne peut être cohérente que sur une surface de courbure constante sur laquelle les « droites » seraient les « géodésiques », c'est-à-dire des trajectoires de cheminement minimum entre deux points.
En conséquence, ne pas admettre le postulat des parallèles d'Euclide conduit simplement à des géométries qui ne s'appliquent pas sur un plan, mais sur des surfaces hyperboliques ou elliptiques.
Ainsi, ce cinquième postulat, « scandale de la géométrie » aux dires de Jean Le Rond d'Alembert, n'exprime pas une vérité absolue, mais relative, quant à l'espace ou plutôt aux espaces possibles de la géométrie.
↑ Retour au haut de cette page