Algorithme CORDIC

Voici une implémentation en PHP 5.6.40 que je vous propose de l'algorithme CORDIC dont la description est détaillée dans le site TrigoFACILE.

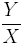
Angle θ demandé : 30 °.

Mesure principale : 30 °, soit 0,5235987755983 radians.

Précision des calculs : 10-15 près.

 

Calculs intermédiaires de tan(30 °) par l'algorithme CORDIC.
k θ restant 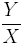Y/X
10,423930123107140,1
10,324261470615970,2020202020202
10,224592818124810,30824742268041
10,124924165633650,42123178385278
10,0252555131424890,54415324819545
20,0152558464558230,55718518950259
20,00525617976915820,57036316860443
30,00425618010249140,5716892390903
30,00325618043582450,57301682664391
30,00225618076915760,57434593652985
30,00125618110249080,5756765740309
30,000256181435823890,57700874444809
40,000156181436157220,57714204604883
45,6181436490554E-50,57727536303724
54,6181436490887E-50,57728869558266
53,6181436491221E-50,577302028282
52,6181436491554E-50,57731536113529
51,6181436491887E-50,57732869414253
56,1814364922206E-60,57734202730372
65,1814364922209E-60,5773433606283
64,1814364922212E-60,57734469395443
63,1814364922216E-60,57734602728209
62,1814364922219E-60,5773473606113
61,1814364922222E-60,57734869394204
61,8143649222258E-70,57735002727433
78,1436492222577E-80,57735016060764
87,1436492222577E-80,57735017394097
86,1436492222577E-80,57735018727431
85,1436492222577E-80,57735020060764
84,1436492222577E-80,57735021394097
83,1436492222577E-80,5773502272743
82,1436492222577E-80,57735024060764
81,1436492222577E-80,57735025394097
81,4364922225771E-90,5773502672743
94,3649222257712.10-100,57735026860764
103,3649222257712.10-100,57735026874097
102,3649222257712.10-100,5773502688743
101,3649222257712.10-100,57735026900764
103,6492222577124.10-110,57735026914097
112,6492222577124.10-110,5773502691543
111,6492222577124.10-110,57735026916764
116,4922225771243.10-120,57735026918097
125,4922225771243.10-120,5773502691823
124,4922225771243.10-120,57735026918364
123,4922225771243.10-120,57735026918497
122,4922225771243.10-120,5773502691863
121,4922225771243.10-120,57735026918764
124,922225771243.10-130,57735026918897
133,922225771243.10-130,5773502691891
132,922225771243.10-130,57735026918924
131,922225771243.10-130,57735026918937
139,2222577124297.10-140,5773502691895
148,2222577124297.10-140,57735026918952
147,2222577124297.10-140,57735026918953
146,2222577124297.10-140,57735026918954
145,2222577124297.10-140,57735026918956
144,2222577124297.10-140,57735026918957
143,2222577124297.10-140,57735026918958
142,2222577124297.10-140,5773502691896
141,2222577124297.10-140,57735026918961
142,2225771242969.10-150,57735026918962
151,2225771242969.10-150,57735026918962
152,2257712429687.10-160,57735026918963

 

L'utilisation de l'algorithme CORDIC a donc permis de calculer la tangente de l'angle de mesure 30 ° au moyen d'opérations élémentaires, en 63 itérations.

Nous avons alors trouvé :

Remarquons la précision de ce calcul en comparant le résultat avec ce que renvoient les fonctions trigonométriques prédéfinies dans PHP :

L'utilisation d'un développement en série entière de Taylor s'avère en général moins précis, et demande beaucoup plus de calculs très compliqués et non optimisés. À titre d'exemple pour la fonction tangente :

Essayer à nouveau l'algorithme CORDIC

Si vous souhaitez réaliser un nouveau calcul, indiquez l'angle souhaité dans la case ci-dessous :

(par exemple « 30 », « 841,274 », « -57 », etc.)