

Et lorsque les lignes qui comprennent cet angle sont des lignes droites, l'angle est appelé rectiligne.
Cette neuvième définition complète la précédente définition d'un angle. La majorité des angles qu'Euclide utilise font partie de cette catégorie d'angles rectilignes.
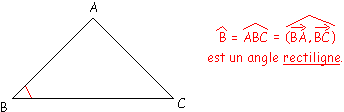
Les angles sont habituellement notés à partir de trois points, le point du milieu étant le point d'origine des deux lignes droites. Il est aussi possible d'utiliser une écriture vectorielle. Néanmoins, lorsqu'il n'existe pas d'ambiguïté, il est suffisant d'écrire l'angle par ce seul point surmonté d'un « chapeau ».
Dans notre exemple, le point B est le point d'origine des deux lignes droites [AB] et [BC].
Selon Euclide, les angles rectilignes ont aussi des « grandeurs » qui peuvent s'ajouter entre elles. Même lorsque la somme de plusieurs angles surpasse un angle plat, l'angle issu de cette somme de « grandeurs » est toujours considéré comme le résultat de cette somme, plutôt qu'un angle individuel inférieur à un angle plat.
En ce qui concerne les mesures d'angles, ni les degrés ni les grades ni les radians n'étaient utilisés à l'époque d'Euclide. Seules les mesures strictement positives d'angles étaient considérées par les mathématiciens grecs. De facto, l'absence d'angle nul et de mesures négatives compliquaient l'étude intuitive de la géométrie – tout en la simplifiant par la même occasion !
↑ Retour au haut de cette page